
Das Standardverfahren zur Authentifizierung ist die Abfrage eines Passworts, zumeist in der Kombination mit einem Nutzernamen.
Selbst wenn andere Authentifizierungsverfahren eingesetzt werden, ist häufig ein Passwort als Alternativmöglichkeit bzw. als Fallbacklösung implementiert.
Die Verwendung von Passwörtern als Authentifizierungsverfahren bietet zahlreiche Angriffsmöglichkeiten, durch die es möglich ist, dass Unberechtigte in den Besitz eines Passworts gelangen können. Maßgeblich für die Sicherheit, also den Schutz vor Erraten durch Dritte, ist die Länge und Zusammensetzung (Komplexität) von Passwörtern. Die relevanten Angriffe auf Passwörter und ihre Einsatzfelder und Gegenmaßnahmen werden in der Folge erläutert.
Als Brute-Force-Angriff bezeichnet man Attacken, bei denen, anders als bei der Verwendung von rainbow tables, durch einfaches Durchprobieren sämtlicher vorhandener Passwörter einer bestimmten Länge und Komplexität versucht wird, das Passwort zu erraten. Das Durchprobieren erfolgt dabei nur nach einer Methode, die verhindert, dass dasselbe Passwort mehrmals getestet wird. Weitere Optimierungen oder Anpassungen gibt es nicht. Deshalb ist die Rede von roher Kraft (brute force). Diese Form wird in der Kryptografie auch exhaustive search genannt, weil im schlechtesten Fall der Gesamtbereich (Keyspace) möglicher Passwörter einer bestimmten „Stärke“ durchprobiert werden muss, bevor das richtige Passwort gefunden wird.
Brute force-Angriffe sind die „simpelste“ Form von Angriffen zum Erraten von Passwörtern, können dafür aber, anders als andere Angriffe, auch in den meisten Szenarien (zumindest in der Theorie) zum Erfolg führen. Brute force-Angriffe und andere Passwortattacken können online oder offline durchgeführt werden.
Um die Gefahren der weiteren Angriffsmethode zu verstehen, ist zunächst die Erläuterung von zwei unterschiedlichen Fällen von Passwortangriffen notwendig, daran anschließend wird der Angriff mit rainbow tables erläutert. Grundsätzlich unterscheidet man zwischen Online- und Offline-Attacken auf Passwörtern.
Bei Online-Angriffen werden die Passwörter direkt an einer Log-in-Maske, z. B. bei einem Server oder einer Anmeldung beim Betriebssystem eines Rechners ausprobiert.
Diese Angriffsversuche fallen in der Regel schnell auf, weil eine Vielzahl von fehlgeschlagenen Anmeldeversuchen registriert wird. Ein Schutzmechanismus gegen diese Form des Angriffs ist etwa das Sperren der Quelle dieser Anmeldeversuche (z. B. einer IP-Adresse, über welche die Anmeldungen gesendet werden).
Diese Schutzmaßnahme hat allerdings den Nachteil, dass die Maßnahme selbst wieder für eine Attacke auf den geschützten Dienst genutzt werden kann, weil durch ein gezieltes Auslösen der Schutzmaßnahme Nutzer oder Dienst- bzw. Administrationsaccounts gesperrt werden können (Denial-of-Service-Angriff). Bei Online-Angriffen bietet sich die direkte Verwendung von rainbow tables nicht an, da hierfür das Passwort selbst im Klartext in die Log-in-Maske eingegeben werden muss.
Offline-Angriffe versuchen, Passwörter aus abgefangenen Informationen über Passwörter zu errechnen. Dies kann die Folge eines data breaches einer Passwort-Datenbank, wie wir sie leider fast täglich erleben, sein oder nachdem Passworthashes bei der Übermittlung mitgeschnitten oder abgefangen wurden. Alle Offline-Angriffe dienen in der Folge dazu, einen solchen Hashwert in den sogenannten Klartext, also ein Passwort, wie es vom Nutzer eingegeben wird, zurückzuführen. Das ist mit sehr großem Aufwand verbunden, weil kryptografisch sichere Hashverfahren Einwegfunktionen sind. Die Funktion kann also nicht einfach umgekehrt werden. Deshalb muss ein Klartext gefunden werden, der durch die Anwendung der entsprechenden Hashfunktion denselben Hashwert liefert. Weil Hashfunktionen niemals kollisionsresistent sind, besteht dabei stets die Möglichkeit, dass verschiedene Eingabewerte denselben Hashwert liefern. Ob es sich um das tatsächliche Passwort handelt, ist somit irrelevant. Der Hashwert wird also erraten. Das „Knacken“ der Hashes ist notwendig, weil Passwörter nicht im Klartext gespeichert werden sollten. Das bedeutet: Ein Server oder andere Funktionen, die ein Passwort prüfen, verfügen selbst nicht über die Klartextversion des Passworts.
Offline-Angriffe, beispielsweise unter Verwendung von rainbow tables, haben für den Angreifer den Vorteil, dass er sehr viel mehr Ressourcen wie Zeit und Rechenleistung auf das Knacken der Passwörter verwenden kann. Dieser Aufwand fällt, anders als bei Online-Attacken nicht auf, weil die Passwörter zunächst in ihren Klartext zurückgeführt werden und erst ein erfolgreich geknacktes Passwort an einer Log-in-Maske verwendet wird.
Eine Form von Offline-Angriffen auf Passwörter sind rainbow table-Angriffe. Diese Angriffe mittels rainbow tables stellen einen Kompromiss zwischen dem benötigten Zeitaufwand und benötigtem Speicherplatz für das Durchführen eines konkreten Versuchs des Knackens von Passwörtern dar. Der verringerte Zeitaufwand pro Angriff auf einen konkreten Passworthash wird dadurch erreicht, dass die sogenannten rainbow tables einmalig und somit bereits lange vor dem eigentlichen Angriffsversuch errechnet werden können.
In der Theorie könnte ein Angreifer für jedes Hashverfahren und eine definierte Menge von möglichen Passwörtern (z. B. alle Passwörter mit einer maximalen Länge von 8 Zeichen, bestehend aus Groß- und Kleinbuchstaben und Zahlen) eine Hash-Tabelle errechnen, in der jedem dieser Passwörter der korrespondierende Hashwert zugeordnet ist. Um einem Hashwert das oder die entsprechenden Passwörter zuzuordnen, muss dann nur noch diese Tabelle nach dem passenden Hash durchsucht werden, was sehr viel schneller geht, als alle Passwörter erneut zu hashen.
Eine Tabelle mit allen möglichen Hashwerten ist aber in der Praxis nicht nutzbar, weil schon bei sehr schwachen Passwörtern der Speicherbedarf für diese Tabelle so groß ist, dass es unmöglich wird, die Informationen abzuspeichern. Durch den Einsatz von rainbow tables kann die Größe der genutzten Tabelle verringert werden, sodass die rainbow table auf modernen Datenträgern abgespeichert werden kann. Der initiale Rechenaufwand für die Erstellung der rainbow table bleibt ähnlich zur Erstellung einer einfachen Hash-Tabelle. Als Kompromiss muss allerdings mit einem höheren (aber akzeptablen) Rechenaufwand während des eigentlichen Angriffsversuchs gerechnet werden. Bei rainbow table-Angriffen handelt es sich deshalb um einen sogenannten Space-time tradeoff, der einen realisierbaren Kompromiss zwischen Rechenaufwand und Speicherbedarf bietet.
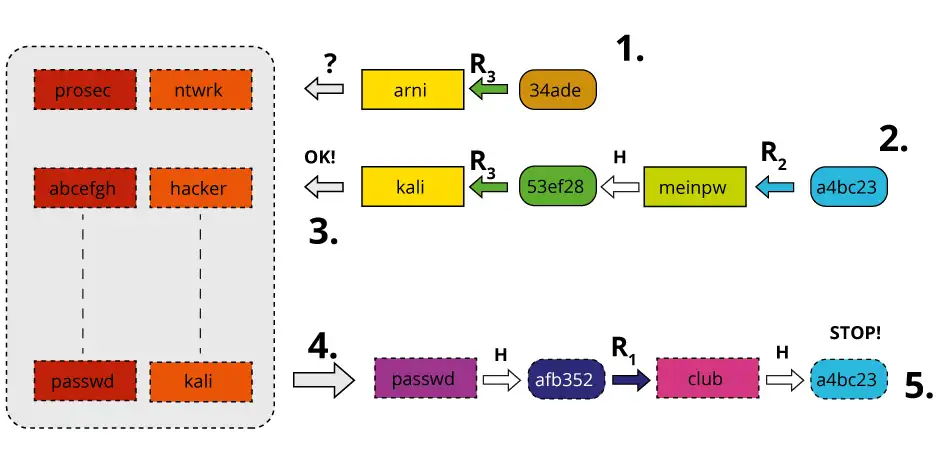
Rainbow tables werden aus Hash-Ketten zusammengesetzt. Dieses Vorgehen basiert auf einer Methode eingeführt von Martin Hellman. Basierend auf einer bestimmten Zahl von möglichen Passwörtern, die als Startpunkt für die Hash-Ketten dienen, werden die Ketten durch das hashen und eine „Reduktion“ des dabei entstehenden Hashwerts in eine Form, die den Passwortkriterien entspricht und dann erneut gehasht werden kann, gebracht. Wichtig hierbei ist, dass es sich bei den Reduktionsfunktionen, die die Reduktion vornehmen, nicht um eine Umkehr des Hashverfahrens handelt, denn eine solche Umkehrfunktion existiert nicht. Die Reduktion macht aus dem Hash, der sehr viel größer als das ursprüngliche Passwort, sprich: sehr viel komplexer, ist lediglich einen Wert, der den Kriterien der Passwortstärke entspricht.
Beispiel: Der beispielhafte Hashwert des „Passworts“ hunter22 lautet
20d2fe5e369db54ec70906 39a9dc30ec4d6086049362 39d39e2de07fda09eb0b
Die Reduktion hiervon könnte darin bestehen, nur die ersten 8 Zeichen des Hashs als nächstes Passwort in der Kette zu verwenden. Diese wären dann „20d2fe5e“ und können als nächster Schritt erneut gehasht werden.
Eine Hash-Kette besteht also aus „sich abwechselnden“ möglichen Passwörtern und deren korrespondierenden Hashwerten. Für sich genommen bietet diese Methode aber noch keinen Vorteil über den theoretischen Einsatz einer einfachen Hash-Tabelle, denn wenn die Hash-Ketten in einem Umfang eingesetzt werden, der alle möglichen Passwörter der entsprechenden Komplexität abdeckt und dann diese Ketten in einer Tabelle abspeichert werden, ist der benötigte Speicherplatz mindestens so groß wie der einer einfachen Hash-Tabelle. Deshalb wird nur der Anfangspunkt, also das erste Passwort und das letzte „Passwort“ also eine letzte Reduktion des zuletzt erstellten Hashwerts einer Kette in einer Tabelle abgespeichert. Die Tabelle besteht also aus einer entsprechenden Zahl von Anfangs- und Endpunkten von Hashketten.
Hat man nun einen Hashwert, kann dieser durch die Anwendung der Reduktionsfunktion darauf getestet werden, ob der Hashwert Teil einer der erstellten Hashketten ist. Hierzu wendet man die Reduktionsfunktion auf den Hashwert an. Ist das Ergebnis der Funktion einer der Endpunkte der Ketten, so hat man die Hashkette gefunden, in der sich das Passwort zum vorhandenen Hashwert befindet. Im gerade beschriebenen günstigsten Falle wäre dieses das vorletzte Passwort in der Kette, welches zum letzten Hashwert in der Kette geführt hat. In der Regel wird man allerdings ein Passwort nicht direkt im ersten Reduktionsschritt finden. Deshalb müssen in der Folge wiederholt die Reduktionsfunktion(en) und die Hashfunktion auf den ursprünglich erbeuteten Hashwert angewendet werden. Man kann sich das beispielhaft so vorstellen, dass man versucht, die den erbeuteten Hashwert enthaltende Hashkette von hinten beginnend wieder zusammen zu setzen. In dem Moment, in dem die teilweise aufgebaute Hashkette einen Endpunkt aufweist, der im rainbow table gespeichert ist, hat man die komplette Hashkette gefunden und kann das Passwort im Klartext extrahieren.
Im Gegensatz zur Methode, die Martin Hellmann vorgeschlagen hat, bei der nur eine Reduktionsfunktion zum Einsatz kommt, nutzen rainbow tables für jeden Reduktionsschritt in der Hashkette eine andere Reduktionsfunktion. Daher stammt der Name rainbow table, weil die Anwendung einer neuen Funktion in jeder Spalte der Tabelle an einen Regenbogen erinnern würde, wenn man die Reduktionsfunktionen in unterschiedlichen Farben darstellen würde. Der Einsatz verschiedener Reduktionsfunktionen in rainbow tables hat den Vorteil, dass Hashkollisionen sehr viel seltener auftreten. Kollisionen bezeichnen den Fall, in dem zwei unterschiedliche Passwörter denselben Hashwert erzeugen. Zwar sind solche Kollisionen sehr selten, weil kryptografische Hashfunktionen die Eigenschaft aufweisen eine hohe Kollisionsresistenz zu haben, aber Kollisionen können niemals ausgeschlossen werden. Tritt eine solche Kollision in einer Hashkette mit nur einer Reduktionsfunktion auf, dann wird der weitere Verlauf der Hashkette stets derselbe sein. Man bezeichnet dies als ein mergen (Verschmelzen) der Hashketten. Die Menge der durch die Ketten abgebildeten Passwörter wird deshalb mit jeder Kollision geringer. Dies hat zur Folge, dass die Effizienz dieser Methode bei steigender Größe des tables immer geringer wird und somit immer mehr Speicherplatz benötigt würde. Der Einsatz von verschiedenen Reduktionsfunktionen in rainbow tables hat zur Folge, dass eine Hashkollision und in der Folge ein Verschmelzen der Ketten nur noch dann auftritt, wenn die Kollision in derselben Spalte der Tabelle auftritt, also beim Einsatz derselben Reduktionsfunktion. Rainbow table sind deshalb effizienter als einfache Tabellen aus Hashketten.
Gegenmaßnahmen bei Angriffen mit rainbow tables sind der Einsatz moderner key derivation functions. Bei diesen handelt es sich um spezielle Hashfunktionen, die für das Hashen von Passwörtern genutzt werden sollten. Vordergründig für den Schutz vor rainbow tables ist hierbei der Einsatz eines sogenannten Salts. Unter einem Salt versteht man einen zufälligen String, der beim ersten Hashen des eingegebenen Passworts mit diesem kombiniert und danach zusammen mit dem Passworthash und dem Nutzernamen gespeichert wird. Wird das Passwort erneut eingegeben, wird jedes Mal der Salt zu der Eingabe hinzugefügt und nur durch diese Kombination kann der korrekte Hash für die Authentifizierung erzeugt werden. Der Salt muss dabei nicht geheim bleiben. Um ein solches Passwort erfolgreich mit einer rainbow table angreifen zu können, müssten die tables für jeden einzelnen möglichen Saltwert vorberechnet werden. Bei einem ausreichend komplexen Salt ist das nicht möglich, weil der Rechenaufwand und Speicherbedarf zu groß sind, um realistisch diese tables berechnen zu können.
Eine weitere Eigenschaft von key derivation functions ist, dass sie das ursprüngliche Passwort wiederholt hashen. Üblich sind hierbei in der Regel zwischen 10.000 und 100.000 Wiederholungen. Bei einem einzelnen Passwort ist der Unterschied in der Dauer des Hashvorgangs für den Anwender kaum zu spüren. Skaliert man den Aufwand aber für die Vorberechnung einer sehr großen Menge an Passwörtern, wird dieser durch den 10.000- bis 100.000-fachen Rechenaufwand selbst bei einem Einsatz von rainbow tables dieser schnell unwirtschaftlich oder sogar unrealistisch.
Eine weitere Maßnahme, die jeder Nutzer selbst in der Hand hat, um einem rainbow table Angriff entgegenzuwirken, ist die Wahl eines ausreichend komplexen Passworts. Durch die Verlängerung von genutzten Passwörtern und den Einsatz von möglichst vielen unterschiedlichen Zeichen steigt die Komplexität des Passworts so schnell an, dass eine Berechnung von rainbow tables ebenso wie das Cracken per Brute Force nicht mehr möglich ist.
Eine Empfehlung hierfür ist eine Passwortlänge von mindestens 12 Zeichen und die Verwendung von Groß- und Kleinbuchstaben, Zahlen und Sonderzeichen. Das Passwort sollte zudem zufällig aus diesen Zeichensätzen kombiniert werden. Da solche sicheren Passwörter nur schwer zu merken sind, sollte stets ein Passwortmanager genutzt werden. Um Nutzer bei der Wahl sicherer Passwörter zu unterstützen, sollte der Umgang mit diesen und den Tools, die bei ihrem Einsatz genutzt werden können, geschult werden. Auch über die Gefahren von trivialen Passwörtern und der Wiederverwendung oder unsicheren Speicherung von Passwörtern sollte der Nutzer sensibilisiert werden.
Obwohl moderne kryptografisch sichere Hashverfahren und key derivation functions heute standardmäßig eingesetzt werden, bieten rainbow tables immer noch einen Nutzen.
Bei der Authentifikation von Windows werden auch heute noch NTLM-Hashes eingesetzt, durch die das Passwort für den Windowszugang gehasht wird. Diese Hashes können z.B. bei einer Kompromittierung eines Firmennetzwerks durch Hacker abgefangen werden.
Weil diese Hashes auf veralteten Hashverfahren basieren, lassen sie sich durch rainbow tables knacken. Auch MD5-Hashes ohne einen Salt können durch rainbow tables geknackt werden.
Wir verwenden Cookies, und Google reCAPTCHA, das Google Fonts lädt und mit Google-Servern kommuniziert. Durch die weitere Nutzung unserer Website stimmen Sie der Verwendung von Cookies und unserer Datenschutzerklärung zu.
